Математика. 9-11 классы. Учебные курсы для индивидуальных образовательных маршрутов учащихся. Программы курсов. Материалы к занятиям. Программа для установки через Интернет
| Код | СИ-752 |
| Авторы-составители | Сагателян А. |
| Издательство | Учитель, 2025 |
| Серия | Образовательные маршруты |
| Электронная версия | скачать |
Инструкция по оплате и установке электронной продукции через Интернет: ознакомиться.
Покупка одного экземпляра программы дает право её использования на одном ПК.
Электронное пособие "Математика. 9-11 классы. Учебные курсы для индивидуальных образовательных маршрутов учащихся" серии "Образовательные маршруты" предлагает несколько структурированных программ действий ученика на фиксированном этапе обучения.
Электронное пособие объединил в себе три учебных пособия:
- "Решение уравнений высших степеней";
- "Решение текстовых задач";
- "Решение задач на комбинацию многогранников и сфер (шаров)".
Каждое учебное пособие включает рабочую программу учебного курса и материалы к занятиям, разработанные в соответствии с требованиями ФГОС (методические рекомендации по организации индивидуального проекта; основные методы решения задач; самостоятельные, проверочные, диагностические работы для оценки текущего и итогового уровня обучения; критерии оценки деятельности учащихся).
Электронное пособие предназначено учителям математики, обучающимся 9-11 классов; рекомендовано абитуриентам вузов.
С этим товаром покупают
Примеры документов
Одночлены и многочлены
1.1. ОДНОЧЛЕНЫ И МНОГОЧЛЕНЫ
Повторяем.
· Выражение, представляющее собой произведение чисел, переменных и их степеней называется одночленом.
Пример 1. 3ах2; –2b 3; 0,5с3; –3b 2.
· Стандартным видом одночлена называется произведение, составленное из числового множителя (коэффициента) и степеней различных переменных.
Пример 2. –2; а; 54; у3; –8а3х4.
· Степенью одночлена стандартного вида называется сумма показателей степеней переменных.
Пример 3. 9х4у3– одночлен степени семь.
· Одночлены, отличающиеся только числовыми коэффициентами или равные между собой, называются подобными.
· Алгебраическая сумма одночленов называется многочленом.
Пример 4. 3а2 – 5ах4 – 3.
· Многочленом стандартного вида называется многочлен, все одночлены которого записаны в стандартном виде. Всякий многочлен можно представить в стандартном виде. Стандартную запись многочлена называют канонической.
Канонический [гр. kanonikos – установленный правилом] – 1) основанный на церковных правилах; установленный церковными канонами; 2) принятый за образец; основанный на каноне; закон, правило.
Пример 5. 2х2у3.
· Степенью многочлена стандартного вида называется наибольшая степень одночлена, входящего в этот многочлен.
Пример 6. 5х2а3 + 2х2а – 5 – многочлен пятой степени.
· Сумму подобных членов можно заменить одним членом, сложив их коэффициенты и оставив ту же буквенную часть. Такое тождественное преобразование многочленов называется приведением подобных членов.
Пример 7. –х4+ 2х3 – 4х4 + 2х2 – 3х2 = –5х4 + 2х3 – х2.
· Произведение двух многочленов равно сумме произведений каждого члена первого многочлена на каждый член второго многочлена.
Пример 8. (х + 2у) (3х2 – у + ху) = 3х3 – ху + х2у + 6ух2 – 2у2 + 2ху2 =
= 3х2 – ху +7ух2 – 2у2 +2ху2.
· Разложить многочлен на множители означает представить его в виде произведения многочленов.
· При разложении многочлена на множители используют метод вынесения общего множителя за скобки, метод группировки членов и формулы сокращенного умножения.
Пример 9. Разложить на множители многочлен 2х2у + у2 – 2х3 – ух.
Решение. Группируя члены и вынося общий множитель за скобки, получим: 2х2у + у2 – 2х3 – ух = (2х2у – 2х3) + (у2 – ух) = 2х2(у – х) + у(у – х) = = (у – х) (2х2 + у).
· Свойства делимости многочленов:
1. Если многочлен Pn(х) делится на многочлен Qm(х), а многочлен Qm(х) делится на многочлен Ri(х), то многочлен Pn(х) делится на Ri(х).
2. Если многочлены Pn(х) и Qm(х) делятся на многочлен Ri(х), то многочлен Pn(х)+ Qm(х) и Pn(х) – Qm(х) делятся на Ri(х), а многочлен Pn(х) ґ Qm(х) делится на R2i(х).
3. Если многочлен Pn(х) делится на многочлен Qm(х), то произведение Pn(х) на любой многочлен Ri(х) также делится на многочлен Qm(х).
4. Многочлены Pn(х) + Qm(х) делятся друг на друга тогда и только тогда, когда Pn(х) = С ґ Qm(х), где С ≠ 0.
5. Если многочлен Pn(х) = Qm(х) × Ri(х) делится на двучлен (х – 2), то хотя бы один из многочленов Qm(х) и Ri(х) делится на (х – 2).
· Строгое определение (для самых продвинутых). Многочленом степени n от переменной х называется функция вида
![]()
где числа ![]() называются коэффициентами многочлена, причем а0 – старший коэффициент, а0 ≠ 0, аn – свободный член. Если а0 = 1, многочлен называется приведенным. Например,
называются коэффициентами многочлена, причем а0 – старший коэффициент, а0 ≠ 0, аn – свободный член. Если а0 = 1, многочлен называется приведенным. Например,
![]() – приведенный многочлен третьей степени.
– приведенный многочлен третьей степени.
Решаем самостоятельно.
1. Вынесите за скобки общий множитель:
а) 7ах + 7х; е) 6а2b + 12аb2;
б) 22у – 11ху; ж) 10а – 15b + 15аb;
в) х3 – х2; з) 2с6 – 15с2;
г) 3х + 6х2; и) 12а2b – 18аb 2 – 3аb2;
д) у4 + 2у3; к) 20х4 – 25х2у2 – 10х3.
2. Разложите на множители:
а) 2у(х – 3) – 5с(3 – х); г) 5ха + 2 + 10х2;
б) а2(х – у) – с(у – х); д) асх2с + асхс;
в) ах + ах + 1; е) 15х2с + 3 – 25хс + 1.
3. Докажите, что:
а) 487 – 486 делится на 47; в) 523 – 521 делится на 24;
б) 488 – 247 делится на 23; г) 257 + 513 делится на 30.
Деление многочлена на многочлен с остатком
1.2. Деление многочлена на многочлен с остатком
Задача деления многочлена на многочлен выполнима не всегда: если заданы многочлены А(х) и В(х), то не всегда найдется многочлен С(х) такой, что А(х) = В(х) Ч С(х). Однако, как и для множества целых чисел, так и для многочленов имеет место деление с остатком.
Например: 25 : 4 = 6 (ост. 1); 25 = 4 Ч 6 + 1.
А(х) : В(х) = С(х) (ост. Р(х)).
А(х) – делимое; В(х) – делитель; С(х) – неполное частное; Р(х) – остаток.
Если А(х) и В(х) многочлены, то выражение вида ![]() называется алгебраической дробью. Алгебраическая дробь называется правильной в том случае, если степень старшего члена числителя меньше степени старшего члена знаменателя, и неправильной, если старшая степень числителя больше или равна старшей степени знаменателя. Всякая неправильная дробь может быть преобразована в сумму некоторого многочлена
называется алгебраической дробью. Алгебраическая дробь называется правильной в том случае, если степень старшего члена числителя меньше степени старшего члена знаменателя, и неправильной, если старшая степень числителя больше или равна старшей степени знаменателя. Всякая неправильная дробь может быть преобразована в сумму некоторого многочлена ![]() – целая часть и правильной дроби
– целая часть и правильной дроби 
Учим наизусть.
Теорема. Пусть А(х) и В(х) многочлены, тогда существуют многочлены С(х) и Р(х) такие, что А(х) = В(х) Ч С(х) + Р(х), причем степень Р(х) меньше степени В(х).
· Для деления многочлена на многочлен применяют запись деления «уголком», аналогичную при делении многозначных чисел.
Алгоритм деления:
1. Расположить делимое и делитель по убывающим степеням х.
2. Разделить старший член делимого на старший член делителя, полученный одночлен является первым членом частного.
3. Первый член частного умножить на делитель и вычесть из делимого, полученная разность является первым остатком.
4. Чтобы получить следующий член частного, надо с первым остатком поступить так же, как поступали с делителем.
Процесс продолжается до тех пор, пока не будет получен остаток, равный нулю, или остаток, степень которого ниже степени делителя. Если остаток равен нулю, то А(х) : В(х).
Например,

т. к. 
Решаем вместе.
Пример 1. Проведите деление с остатком:
2х4 + х3 – 5х2 – х + 1 на х2 – х.
Решение.

Третий остаток имеет степень ниже степени делителя, следовательно, процесс деления завершен.
С(х) = 2х2 + 3х – 2; Р(х) = –3х + 1.
Данный многочлен можно записать в виде:
2х4 + х3 – 5х2 – х + 1 = (х2 – х)(2х2 + 3х – 2) + (–3х + 1)
или

Пример 2. Проведите деление с остатком:
2х6 – 3х4 – 5х3 + х – 6 на х4 + 3х3 + 5.
Решение.
Поделим многочлен «уголком».
Теорема Безу. Корни многочлена
1.3. ТЕОРЕМА БЕЗУ. КОРНИ МНОГОЧЛЕНА
Историческая справка.
Этьен Безу (уроженец Немура, 1730–1783 гг.) – французский математик, член Парижской Академии Наук с 1758 года. С 1763 года Безу преподавал математику в училище гардемаринов, а с 1768 года и в королевском артиллерийском корпусе.
Основные работы Этьена Безу относятся к высшей алгебре, они посвящены созданию теории решения алгебраических уравнений. В теории решения систем линейных уравнений ученый содействовал возникновению теории определителей, развивал теорию исключения неизвестных из систем уравнений высших степеней, доказал теорему (впервые сформулированную К. Маклореном) о том, что две кривые порядка m и n пересекаются не более чем в mn точках. Во Франции и за ее границами, вплоть до 1848 года был популярен его шеститомный «Курс математики», написанный им в 1764–1769 годах. Безу развил метод неопределенных множителей, в элементарной алгебре его именем назван способ решения систем уравнений, основанный на этом методе. Часть трудов Безу посвящена внешней баллистике. Именем ученого названа одна из основных теорем алгебры.
· Если при делении многочлена на многочлен А(х) : В(х) в качестве делителя В(х) рассматривать двучлен, степень которого равна 1, то степень остатка должна быть равна нулю, т. е. остаток должен быть некоторым числом r, т. е. А(х) = (х – а) М(х) + r. Найдем r. Положим в этом тождестве х = а, получим А(а) = (а – а) М(а) + r, значит, r = А(а).
Учим наизусть.
Теорема 1. (Теорема Безу). Остаток от деления многочлена А(х) на двучлен х – а равен А(а), число а называют корнем многочлена А(х), если А(а) = 0.
Теорема Безу позволяет, не выполняя операцию деления, определить, является ли данное число корнем многочлена.
Решаем вместе.
Пример 1. Показать, что числа 2 и –2 являются корнями многочлена
х4– 4х3 + х2 + 16х – 20.
Решение.
Пусть А(х) = х4 – 4х3 + х2 + 16х – 20.
А(–2) = (–2)4 – 4(–2)3 + (–2)2 + 16(–2) – 20;
А(–2) = 16 + 32 + 4 – 32 – 20;
А(–2) = 0 – корень многочлена.
А(2) = 24 – 4 ∙ 23 + 22 16 ∙ 2 – 20;
А(2) = 16 – 32 + 4 + 32 – 20;
А(2) = 0 – корень многочлена.
Итак, числа 2 и –2 являются корнями многочлена х4– 4х3 + х2 + 16х – 20.
Учим наизусть.
Теорема 2. Число а является корнем многочлена А(х) в том и только в том случае, когда А(х) делится на х – а.
Решаем вместе.
Пример 2. Покажем, что многочлен х4– 4х3 + х2 + 16х – 20 делится на х – 2.
Решение.
Воспользуемся делением «уголком».

Итак, многочлен х4– 4х3 + х2 + 16х – 20 делится на двучлен х – 2 без остатка, следовательно, х = 2 – корень многочлена.
Пример 3. Выполнить деление многочлена ![]() на многочлен
на многочлен ![]()
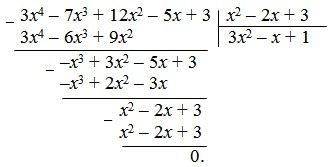
Следовательно, ![]()
Учим наизусть.
Теорема 3. Если числа а1, а2……ак различны, то многочлен А(х) делится на (х – а1); (х – а2);….(х – ак). Эти числа являются корнями многочлена А(х).
Следствие 1. Многочлен степени n не может иметь более чем n различных корней.
Теорема Виета
1.6. ТЕОРЕМА ВИЕТА
Историческая справка.
Франсуа Виет. Знаменитый математик Франсуа Виет родился в 1540 году (1540–1603) в небольшом городке Фантанеле-Конт на юге Франции. Юрист по образованию, Виет служил при дворе Генриха IX. Математикой занимался в часы отдыха. Ознакомившись с учением Коперника, Виет заинтересовался астрономией и решил написать обширный астрономический трактат, но для этого надо было глубоко знать математику. Занявшись изучением математики, он выполнил ряд алгебраических исследований, разработал символику в алгебре, но трактата по астрономии так и не написал. Свою знаменитую теорему, которая известна под названием терема Виета, он доказал в 1591 году. Люди пользуются этой теоремой уже пятое столетие. Франсуа Виет обладал огромной трудоспособностью, он мог работать по трое суток без отдыха, многие его результаты и открытия достойны восхищения.
Во время войны Франции с Испанией Виет оказал большую услугу своей родине – он расшифровал весьма важное письмо испанского двора. Правители Испании, письмо которых было перехвачено, не допускали мысли, что такой сложный шрифт может быть раскрыт. Впоследствии они приписали раскрытие их шрифта волшебству чародея.
В работе «Введение в аналитическое искусство» Ф. Виет изложил усовершенствованную им теорию уравнений с применением изобретенных символов. В названном трактате Виет использовал алгебраические выкладки при рассмотрении вопросов геометрии.
Виет ввел в алгебру общую символику. Числовые коэффициенты он стал обозначать согласными буквами и придумал новый термин – коэффициент, позаимствовав из латинского языка слово coefficiens – «содействующий». Знаки «+» и «–» он употреблял в современном значении, неизвестные обозначал буквами латинского алфавита.
Учим наизусть.
Теорема Виета. Сумма корней приведенного уравнения степени n равна второму коэффициенту с противоположным знаком, сумма различных произведений корней, взятых по два, равна третьему коэффициенту, сумма различных произведений корней, взятых по три, равна четвертому коэффициенту, взятому с противоположным знаком, и т. д., а произведение корней равно свободному члену со знаком, равным (–1)n:

Для уравнения третьей степени х3 + рх2 + qх + r = 0, если х1; х2; х3 – корни, справедливы следующие формулы:
х1 + х2 + х3 = –p,
х1х2 + х1х3 + х2х3 = q,
х1х2х3 = –r.
При решении уравнений высших степеней применяют два основных метода:
1) разложение на множители;
2) введение новой переменной.
Для решения уравнения а0хn + а1хn – 1 + … + аn – 1х + аn = 0, где а0 ≠ 0 надо разложить многочлен, стоящий в левой части равенства, на множители, что в данном случае является равнозначной операцией – найти корни многочлена.
Решаем вместе.
Пример 1. Решить уравнение 6х3 + 13х2 – 14х + 3 = 0.
Решение.
Делители свободного члена: ±1; ±3; натуральные делители старшего коэффициента: 1; 2; 3; 6. Корни уравнения будем искать среди чисел:
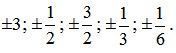
Подставляя их поочередно, обнаруживаем, что корнями являются:
х1 = –3; –162 + 117 + 42 + 3 = 0;
х2 = ![]() ;
; ![]() – 7 + 3 = 0;
– 7 + 3 = 0;
х3 = ![]() ;
; ![]() + 3 = 0.
+ 3 = 0.
Ответ: –3; ![]() ;
; ![]() .
.
Пример 2. Решить уравнение х4 – х3 – 13х2 + х + 12 = 0.
Решение. Очевидно, х1 = 1; х2 = –1
Двучленные уравнения
2.2. ДВУЧЛЕННЫЕ УРАВНЕНИЯ
Учим наизусть.
Уравнение вида axn + b = 0 называется двучленным уравнением. Решение такого уравнения сводится к извлечению корня степени n из числа ![]() Если n – четное и
Если n – четное и ![]() < 0, то действительных корней нет.
< 0, то действительных корней нет.
Решаем вместе.
Пример. Решить уравнение 2х3 + 5 = 0.
Решение. Разложим выражение в левой части уравнения на множители, получаем  Из первого сомножителя, содержащего х, находим
Из первого сомножителя, содержащего х, находим 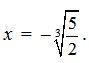 Квадратное уравнение
Квадратное уравнение  действительных корней не имеет.
действительных корней не имеет.
Ответ: ![]()
Продолжайте заполнять таблицу.
Проверяем себя.
Математический диктант
1. Какие уравнения являются целыми?
а) ![]() – 5 = 0; б)
– 5 = 0; б) ![]() = 2; в)
= 2; в) ![]() = 7; г)
= 7; г) ![]() = х.
= х.
2. Какие уравнения являются биквадратными?
а) х4 + 2х + 1 = 0;
б) х4 – 2х2 = 6;
в) х4 – х3 + 1 = 0;
г) х2 = 2х4 + 1.
3. Какие из уравнений решаются методом введения новой переменной?
а) 3х3 – х2 = 0;
б) 2х4 – 3х2 = 1 = 0;
в) (х2 + 1)2 + 2(х2 + 1) – 7 = 0;
г) х3 + 2х2 + х = 0.
4. Уравнение имеет один корень:
а) х2 = –3; б) х2 = 9; в) 2х2 = 0; г) х3 = –8.
5. Уравнения являются равносильными:
а) 5х2 – 5 = 0 и х – 1 = 0;
б) 3х2 = –1 и 2х2 + 4 = 1;
в) 15х2 – 5х + 20 = 0 и 3х2 – х + 4 = 0.
Ответы: 1) а, в; 2) б, г; 3) б, в; 4) г; 5) б, в.
Товар размещен в разделах
QR-код страницы
Для партнеров
с учмагом












