Алгебра 8 класс: поурочные планы по учебнику Ю. Н. Макарычева. Программа для установки через Интернет
| Код | СИ-232.3 |
| Авторы-составители | Дюмина Т. Ю., Махонина А. А. |
| Издательство | Учитель, 2025 |
| Серия | Поурочное планирование |
| Электронная версия | скачать |
Инструкция по оплате и установке электронной продукции через Интернет: ознакомиться.
Покупка одного экземпляра программы дает право её использования на одном ПК.
Конспекты уроков, представленные на диске, систематизированы по разделам в соответствии с распределением учебного материала в учебнике. Предлагаемые поурочные планы включают теоретические материалы, алгебраические задачи с решениями и ответами, задания для устной работы, тесты, проверочные и контрольные работы, математические диктанты и др. В каждом из разделов представлены методические рекомендации к объяснению нового материала.
Целью данного пособия является практическая помощь учителю математики, особенно молодому, в выборе путей построения урока, отвечающего современным требованиям, в подборе дополнительного дидактического материала и проведении проверочных работ.
Компакт-диск предназначен преподавателям математики, может быть полезен студентам педагогических учебных заведений.
С этим товаром покупают
Примеры документов
Урок 2 (4). Сокращение дробей
У р о к 2 (4)
Сокращение дробей
Цели: формировать умение применять основное свойство дроби при сокращении дробей.
Ход урока
I. Организационный момент.
II. Устная работа.
– Сократите дробь:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е) ![]() ; ж)
; ж) ![]() ; з)
; з) ![]() .
.
III. Объяснение нового материала.
Для успешной работы учащихся на уроке им необходимо не только использовать основное свойство дроби, но и применять ряд других знаний и умений, полученных и сформированных ранее.
Учащиеся должны помнить формулы сокращенного умножения и основные приёмы разложения многочлена на множители. Поэтому начать необходимо с актуализации знаний и умений.
З а д а н и я и в о п р о с ы учащимся:
1. Какие существуют способы разложения многочлена на множители?
2. В чём состоит каждый из этих способов?
3. Разложите на множители многочлен:
а) х2у – 2х; д) х2 + 6х + 9;
б) 3a2b – 9ab2; е) а2 – 10а + 25;
в) т2 – 4п; ж) ax + bx + ay + by.
г) а3 – а; з) ab – b + 3a – 3.
После проведения этой работы следует разобрать пример 3 из учебника и сделать в ы в о д: чтобы сократить рациональную дробь, нужно сначала разложить на множители её числитель и знаменатель.
IV. Формирование умений и навыков.
1. № 29, № 30 (а, в, д), № 32 (а, в).
2. № 31, № 34.
3. № 35 (а, в).
Р е ш е н и е
а) 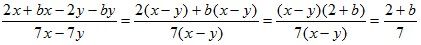 .
.
в) 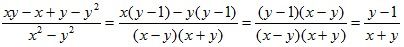 .
.
Д о п о л н и т е л ь н о можно выполнить № 36 (а).
Р е ш е н и е
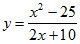
Областью определения этой функции является множество всех чисел, кроме х = –5. Сократим дробь, задающую функцию:
 .
.
Графиком функции ![]() является прямая, а графиком функции
является прямая, а графиком функции  – та же прямая, но с «выколотой» точкой (–5; –5).
– та же прямая, но с «выколотой» точкой (–5; –5).

V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– В чём состоит основное свойство дроби?
– Когда применяется основное свойство дроби?
– Что нужно сделать, чтобы сократить рациональную дробь?
– Какие существуют способы разложения многочлена на множители?
Домашнее задание: № 30 (б, г, е), № 32 (б, г), № 33, № 35 (б, г).
Д о п о л н и т е л ь н о: № 36 (б).
Урок 3 (5). Следствие из основного свойства дроби
У р о к 3 (5)
Следствие из основного свойства дроби
Цели: продолжить формирование умения сокращать дроби; вывести следствие из основного свойства дроби и формировать умение его применять при сокращении дробей.
Ход урока
I. Организационный момент.
II. Устная работа.
– Сократите дробь:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е) ![]() ; ж)
; ж) ![]() ; з)
; з) ![]() .
.
III. Проверочная работа.
В а р и а н т 1
1. Приведите дроби к указанному знаменателю:
а)  ; б)
; б)  ; в)
; в) ![]() .
.
2. Сократите дробь:
а) ![]() ; б)
; б) ![]() .
.
В а р и а н т 2
1. Приведите дроби к указанному знаменателю:
а)  ; б)
; б) ![]() ; в)
; в)  .
.
2. Сократите дробь:
а) ![]() ; б)
; б)  .
.
IV. Объяснение нового материала.
Специальное внимание на этом уроке необходимо уделить следствию из основного свойства дроби.
При объяснении материала следует провести аналогию с обыкновенными дробями. Для этого целесообразно предложить учащимся выполнить з а д а н и е: среди данных дробей найти такие, которые равны ![]() ; ответ объяснить.
; ответ объяснить.
![]() .
.
Здесь же следует вспомнить, что «минус» перед дробью можно записывать как перед числителем, так и перед знаменателем. Для этого дать учащимся такое задание: среди данных дробей найти такие, которые равны ![]() ; ответ объяснить.
; ответ объяснить.
![]() .
.
После выполнения этих заданий можно перейти к буквенной записи следствия из основного свойства дроби:

Необходимо, чтобы учащиеся знали и осознавали формулировку этого следствия. В случае затруднений можно продемонстрировать практическое применение следствия и дать его более прикладную к задачам формулировку:
1. «Минус» перед дробью можно вносить либо в числитель, либо в знаменатель дроби.
П р и м е р:
![]() .
.
 .
.
2. «Минус» из числителя или знаменателя дроби можно выносить за знак дроби.
П р и м е р:
![]() .
.
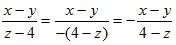 .
.
V. Формирование умений и навыков.
1. № 38, № 39.
2. № 40 (а, в, д, ж), № 41, № 44 (а, в).
Урок 1 (6). Правило сложения и вычитания дробей с одинаковыми знаменателями
У р о к 1 (6)
Правило сложения и вычитания дробей
с одинаковыми знаменателями
Ход урока
I. Организационный момент.
II. Устная работа.
– Вычислите:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; е)
; е) ![]() ; ж)
; ж) ![]() ; з)
; з) ![]() .
.
III. Объяснение нового материала.
Устная работа дает возможность актуализировать знания учащихся о сложении и вычитании обыкновенных дробей с одинаковыми знаменателями.
После этой работы следует сообщить учащимся, что рациональные дроби с одинаковыми знаменателями складываются и вычитаются по тем же правилам, которые учащиеся способны сформулировать самостоятельно.
После формулировки правил на доску выносится их буквенная запись:
 и
и  .
.
Далее следует рассмотреть примеры 1–3 из учебника. Вопрос о сложении и вычитании дробей с противоположными знаменателями целесообразно рассмотреть на следующем уроке.
IV. Формирование умений и навыков.
1. № 53, № 55, № 57.
При вычитании дробей учащиеся могут допускать распространенную ошибку: не учитывать, что «минус» перед дробью вносится в числитель, и неправильно расставлять знаки.
Поэтому важно следить, чтобы первое время учащиеся вели подробные записи.
№ 57.
в) ![]()
= 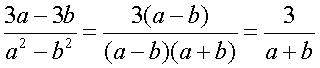 .
.
2. № 58 (а), № 59 (а).
3. № 60.
Р е ш е н и е

= 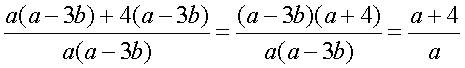 .
.
При а = –0,8 дробь ![]() равна –4, то есть данное в условии значение b является лишним.
равна –4, то есть данное в условии значение b является лишним.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Сформулируйте правило сложения рациональных дробей с одинаковыми знаменателями.
– Сформулируйте правило вычитания рациональных дробей с одинаковыми знаменателями.
Домашнее задание: № 54, № 56, № 59 (б).
Урок 2 (7). Сложение и вычитание дробей с противоположными знаменателями
У р о к 2 (7)
Сложение и вычитание дробей
с противоположными знаменателями
Цели: формировать умение складывать и вычитать рациональные дроби с противоположными знаменателями.
Ход урока
I. Организационный момент.
II. Устная работа.
– Вычислите:
а) ![]() ; д)
; д) ![]() ;
;
б) ![]() ; е)
; е) ![]() ;
;
в) ![]() ; ж)
; ж) ![]() ;
;
г) ![]() ; з)
; з) ![]() .
.
III. Объяснение нового материала.
Сначала необходимо, чтобы учащиеся вспомнили следствие из основного свойства дроби, и предложить им выполнить задание, в котором нужно поменять знак числителя или знаменателя рациональной дроби.
а)  ; в)
; в) ![]() ;
;
б) ![]() ; г)
; г) ![]() .
.
Затем продемонстрировать пример 4 из учебника и сделать вывод о том, как сложить или вычесть две рациональные дроби с противоположными знаменателями.
IV. Формирование умений и навыков.
1. Выполните сложение или вычитание дробей:
а) ![]() ; в)
; в) ![]() ;
;
б) ![]() ; г)
; г)  .
.
2. № 61, № 63.
3. Преобразуйте выражение:
а)  ;
;
б)  ;
;
в)  ;
;
4. № 66.
5. № 68.
Р е ш е н и е
 .
.
Полученное выражение принимает натуральные значения, если дробь ![]() является натуральным числом, то есть когда 6 делится на п. Значит, п = 1; 2; 3; 6.
является натуральным числом, то есть когда 6 делится на п. Значит, п = 1; 2; 3; 6.
О т в е т: 1; 2; 3; 6.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Сформулируйте правило сложения и вычитания рациональных дробей с одинаковыми знаменателями.
– Как выполнить сложение или вычитание рациональных дробей, знаменатели которых являются противоположными выражениями?
Домашнее задание: № 62, № 64, № 67.
Д о п о л н и т е л ь н о: № 69.
Урок 1 (8). Правило сложения и вычитания дробей с разными знаменателями
У р о к 1 (8)
Правило сложения и вычитания дробей
с разными знаменателями
Цели: формировать умение приводить рациональные дроби к общему знаменателю и выполнять их сложение и вычитание.
Ход урока
I. Организационный момент.
II. Проверочная работа.
В а р и а н т 1
Выполнить сложение и вычитание дробей:
а) ![]() ; г)
; г) ![]() ;
;
б) ![]() ; д)
; д) ![]() .
.
в) ![]() ;
;
В а р и а н т 2
Выполнить сложение и вычитание дробей:
а) ![]() ; г)
; г) ![]() ;
;
б) ![]() ; д)
; д) ![]() .
.
в) ![]() .
.
III. Устная работа.
– Найдите наименьший общий знаменатель дробей:
а) ![]() и
и ![]() ; е)
; е) ![]() и
и ![]() ;
;
б) ![]() и
и ![]() ; ж)
; ж) ![]() и
и ![]() ;
;
в) ![]() и
и ![]() ; з)
; з) ![]() и
и ![]() ;
;
г) ![]() и
и ![]() ; и)
; и) ![]() и 0,1;
и 0,1;
д) ![]() и
и ![]() ; к)
; к) ![]() и
и ![]() .
.
IV. Объяснение нового материала.
Приведение алгебраических дробей к общему знаменателю зачастую вызывает у учащихся трудности. При объяснении этого вопроса можно использовать аналогию с обыкновенными дробями.
В процессе проведения устной работы у учащихся была возможность вспомнить, как найти общий знаменатель обыкновенных дробей. После устной работы следует выделить три случая, которые возникают при нахождении общего знаменателя, и привести аналогичные примеры с алгебраическими дробями.
С л у ч а й 1. Знаменатели дробей не имеют общих делителей.
В этом случае наименьший общий знаменатель равен произведению знаменателей дробей.
О б ы к н о в е н н ы е д р о б и:
![]() .
.
Р а ц и о н а л ь н ы е д р о б и:
1) ![]() .
.
2) 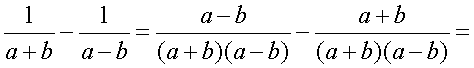
=  .
.
С л у ч а й 2. Знаменатель одной из дробей является делителем знаменателя второй дроби.
В этом случае знаменатель, который делится на другой, является наименьшим общим знаменателем дробей.
О б ы к н о в е н н ы е д р о б и:
![]() .
.
Р а ц и о н а л ь н ы е д р о б и:
1) ![]() ;
;
2) 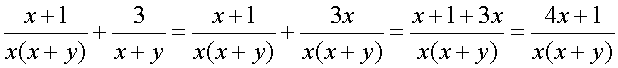 .
.
Товар размещен в разделах
QR-код страницы
Для партнеров
с учмагом









